LA LÓGICA COMPUTACIONAL

La lógica computacional es la misma lógica matemática aplicada al contexto de las ciencias de la computación. Su uso es fundamental a varios niveles: en los circuitos computacionales, en la programación lógica y en el análisis y optimización (de recursos temporales y espaciales) de algoritmos
CIRCUITOS COMPUTACIONALES
El nivel menos abstracto dentro de una computadora está constituido por circuitos electrónicos que responden a diferentes señales eléctricas, siguiendo los patrones de la lógica booleana; esto es, compuertas lógicas que devuelven un valor dependiendo de las entradas que se le dan al sistema. Existen ocho compuertas lógicas básicas con las cuales se pueden formar sistemas muy complejos: AND, OR, Inverter, Buffer, NAND, NOR, XOR y XNOR. Todas ellas son representadas mediante un símbolo y una tabla de valores de verdad, que es simplemente un cuadro donde se ubican todas las posibles entradas y los valores que devolvería la compuerta dados dichos valores.
Todo sistema computacional, por muy complejo que sea, no está compuesto por más que circuitos electrónicos que únicamente entienden un lenguaje binario. La lógica computacional se encarga de modelar y optimizar tales sistemas a este nivel.

DEFINICIÓN DE ALGORITMO:
Define algoritmo como un conjunto ordenado y finito de operaciones que permite hallar la solución de un problema. Método y notación en las distintas fórmulas del cálculo. El algoritmo constituye un método para resolver un problema mediante una secuencia de pasos a seguir. Dicha secuencia puede ser expresada en forma de diagrama de flujo con el fin de seguirlo de una forma más sencilla.
De acuerdo con el concepto anterior, el algoritmo podría estar incluido en la definición de programa de ordenador de la Ley de Propiedad Intelectual (TRLPI), al referirse a éste como toda secuencia de instrucciones o indicaciones destinadas a ser utilizadas, directa o indirectamente, en un sistema informático para realizar una función o una tarea o para obtener un resultado determinado, cualquiera que fuere su forma de expresión y fijación.


La resolución de problemas: es la fase que supone la conclusión de un proceso más amplio que tiene como pasos previos la identificación del problema y su modelado. Por problema se entiende un asunto del que se espera una solución que dista de ser obvia a partir del planteamiento inicial. El matemático G.H. Wheatley lo definió de forma ingeniosa: «La resolución de problemas es lo que haces cuando no sabes qué hacer».1
La resolución de problemas reside principalmente en dos áreas: la resolución de problemas matemáticos y la resolución de problemas personales —en los que se presenta algún tipo de obstáculo a su resolución—,2 mientras que los fundamentos son estudiados en psicología del pensamiento, ciencia cognitiva y teoría de la decisión.


Aquí os dejamos una serie de ejercicios resueltos (14 en total) y con su explicación a modo de ejemplos de construcción de diagramas de flujo de procesos. Si no tienes claro la teoría te recomendamos primero que veas este enlace: Diagramas de Flujo.
1. Hacer el diagrama de flujo para sumar dos números leídos por teclado y escribir el resultado.

1. Hacer el diagrama de flujo para sumar dos números leídos por teclado y escribir el resultado.

2. Hacer un diagrama de flujo que permita leer 2 números diferentes y nos diga cual es el mayor de los 2 números.
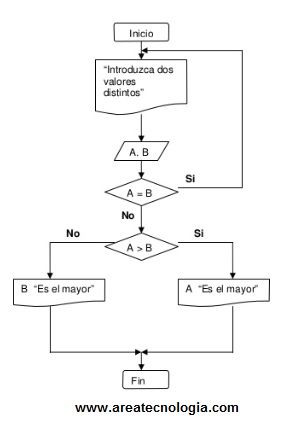
El pseudocódigo para este diagrama sería:

3. Crear un diagrama de flujo de procesos en el que se almacenen 3 números en 3 variables A, B y C. El diagrama debe decidir cual es el mayor y cual es el menor.
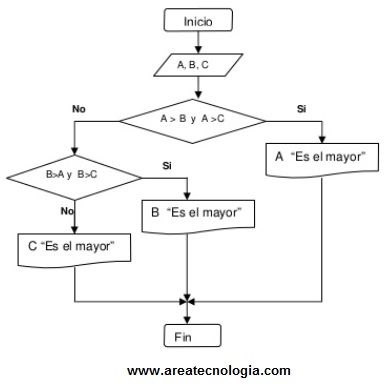

El pseudocódigo para este diagrama sería:

3. Crear un diagrama de flujo de procesos en el que se almacenen 3 números en 3 variables A, B y C. El diagrama debe decidir cual es el mayor y cual es el menor.

4. Realizar el diagrama de flujo para que nos calcule la hipotenusa de un triángulo rectángulo, conocidos su dos catetos.
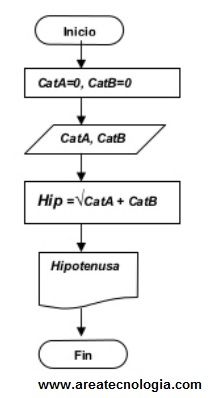
5. Diagrama de Flujo para sumar 100 números leídos por teclado.
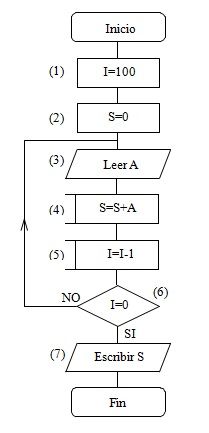
Explicación:
- En I contamos los números que quedan por sumar.
- En S calculamos la suma.
- A se emplea para leer temporalmente cada número.
Vamos a ver paso a paso como funciona. Supongamos que los datos son: 7, -1, 8, 5, ...
(1) I=100 (números a sumar)
(2) S=0 (suma, inicialmente 0) (3) Leer A. El primero es 7, luego A=7 (4) S=S+A=0+7=7
(5) I=I-1=100-1=99 (6) ¿I=0? ® NO
(3) Leer A, ahora A=-1
(4) S=S+A=7-1=6
(5) I=I-1=99-1=98
(6) ¿I=0? ® NO
Cuando I=0 habremos sumado los 100 números y pasaremos a: (7) Escribir S que será la suma.
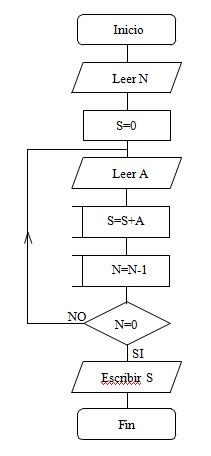
6. Modificar el anterior para que permita sumar N números. El valor de N se debe leer previamente por teclado.
7. Hacer un diagrama de flujo que permita escribir los 100 primeros pares.
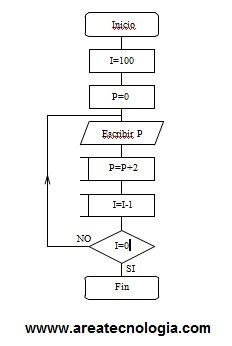
Explicación de la solución:
P: Variable para contener el siguiente par que se debe escribir.
I: Contador de pares que quedan por escribir.
El proceso es similar al anterior. Necesitamos un bucle para contar 100 veces y dentro de él escribimos el par e incrementamos para obtener el siguiente.
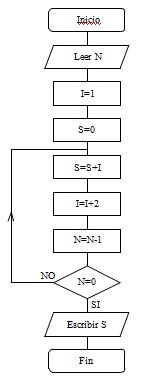
8. Hacer el diagrama de flujo para sumar los N primeros impares. Realizar después uno que haga lo mismo con los pares y otro con los múltiplos de 3.
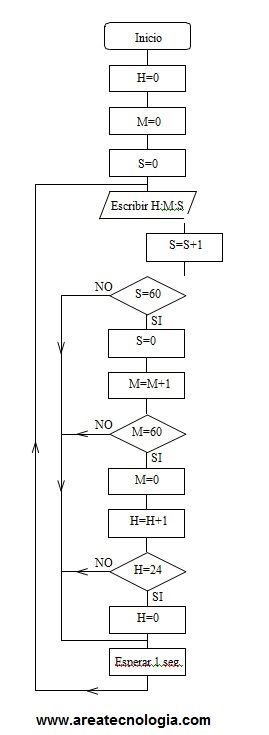
9. Hacer un diagrama de flujo que simule un reloj.

5. Diagrama de Flujo para sumar 100 números leídos por teclado.

Explicación:
- En I contamos los números que quedan por sumar.
- En S calculamos la suma.
- A se emplea para leer temporalmente cada número.
Vamos a ver paso a paso como funciona. Supongamos que los datos son: 7, -1, 8, 5, ...
(1) I=100 (números a sumar)
(2) S=0 (suma, inicialmente 0) (3) Leer A. El primero es 7, luego A=7 (4) S=S+A=0+7=7
(5) I=I-1=100-1=99 (6) ¿I=0? ® NO
(3) Leer A, ahora A=-1
(4) S=S+A=7-1=6
(5) I=I-1=99-1=98
(6) ¿I=0? ® NO
Cuando I=0 habremos sumado los 100 números y pasaremos a: (7) Escribir S que será la suma.
6. Modificar el anterior para que permita sumar N números. El valor de N se debe leer previamente por teclado.

7. Hacer un diagrama de flujo que permita escribir los 100 primeros pares.

Explicación de la solución:
P: Variable para contener el siguiente par que se debe escribir.
I: Contador de pares que quedan por escribir.
El proceso es similar al anterior. Necesitamos un bucle para contar 100 veces y dentro de él escribimos el par e incrementamos para obtener el siguiente.
8. Hacer el diagrama de flujo para sumar los N primeros impares. Realizar después uno que haga lo mismo con los pares y otro con los múltiplos de 3.

9. Hacer un diagrama de flujo que simule un reloj.

JOSÉ ALEJANDRO MARTINEZ MARTINEZ
GRUPO: 1104
MODULO: RESOLUCIÓN DE PROBLEMAS